Bézier curves in OpenSCAD

Writing cookie cutters made me explore Bézier curves, and since I was unsatisfied with the OpenSCAD code I found online, I wrote my own and made a tutorial video.

In this article, I describe the same things as in the video, you have the choice whether you want to watch or read.

The code from the video can be found in this repository in the folder 'teaching examples'.

Essentially, a Bézier curve is a curve described by a couple of points and a formula, and is used in computer graphics, for instance typography. In case of a cookie cutter, I use it to model things that are curvy but not exactly round like a circle or ellipse.

In mathematics, things can be infinite and curves can be perfectly smooth, but in computer graphics curvy things are approximated by points and tiny flat surfaces. This is why in the algorithms used, I calculate many points as the basis of what is going on.

In the (not very useful) case of a Bézier curve that is only defined by the end points and no middle-points that curve it, it could be calculated like this:

// two points
p1 = [5, 7.5];
p2 = [7, 2];

// how many points will be calculated
n = 15;

// calculating points between p1 and p2
for (i = [0 : 1/n : 1])
  translate( p1 * i + p2 * (1-i) )
    sphere(0.2);

// highlighting the control points
for (i = [p1, p2]) translate(i)
  color("black") sphere(0.2);

Please copy the code into OpenSCAD to watch it rendered.

If a third point gets added, the curve gets curvy. The formula 'p1 · [0...1] + p2 · [1...0]' gets called recursively.

p1 = [5, 7.5];
p2 = [7, 2];
p3 = [1, 1.7];
n = 15;

// a Bézier curve [p1, p2, p3]
for (i = [0 : 1/n : 1])
  translate(
      (p1 * i + p2 * (1-i)) * i
    + (p2 * i + p3 * (1-i)) * (1-i) )
      sphere(0.2);

// highlighting the control points
for (i = [p1, p2, p3]) translate(i)
  color("black") sphere(0.2); 

So far we had n = 15 points, but the amout of points we want in production varies. Sometimes we want a specific amount, sometimes their distance matters more than the amount.

We will either be calling the function with that number or rely on the length of the curve and a global variable 'fs'. I have approximations for Bézier curve lengths defined by three, four and control points.

The code below can be found on GitHub.

// roughly the size of parts of curves,
// is a global value
fs = 0.5;

// distance between two points
function dist(a, b) = len(a)==2?
sqrt(                 // two dimensions
    (a[0]-b[0])^2
    +(a[1]-b[1])^2
    ):
sqrt(                 // three dimensions
    (a[0]-b[0])^2
    +(a[1]-b[1])^2
    +(a[2]-b[2])^2
    );

// length of curve
  function length(pts) = [
    // three control points
    if (len(pts) == 3)
        0.43 * dist(pts[0], pts[1])
      + 0.53 * dist(pts[0], pts[2])
      + 0.43 * dist(pts[1], pts[2])
    // four control points
    else if (len(pts) == 4)
        0.35 * dist(pts[0], pts[1])
      + 0.40 * dist(pts[0], pts[2])
      + 0.23 * dist(pts[0], pts[3])
      - 0.09 * dist(pts[1], pts[2])
      + 0.40 * dist(pts[1], pts[2])
    // five control points
    else if (len(pts) == 5)
        0.32 * dist(pts[0], pts[1])
      + 0.35 * dist(pts[0], pts[2])
      + 0.23 * dist(pts[0], pts[3])
      + 0.10 * dist(pts[0], pts[4])
      - 0.13 * dist(pts[1], pts[2])
      + 0.20 * dist(pts[1], pts[3])
      + 0.23 * dist(pts[1], pts[4])
      - 0.13 * dist(pts[2], pts[3])
      + 0.35 * dist(pts[2], pts[4])
      + 0.32 * dist(pts[3], pts[4])
    else
        echo("Wrong number of points")]
  [0];       // makes list into number 

With the amount of points decidable, let's calculate them!

// calculate singular points
function b_pts(pts, fn, idx) =
  // has pts more than two points?
  len(pts) > 2 ?
  // it calls itself in smaller portions
    b_pts([for(i=[0:len(pts)-2])
        pts[i]], fn, idx) * fn*idx
      + b_pts([for(i=[1:len(pts)-1])
        pts[i]], fn, idx) * (1-fn*idx)
  // at two points we do the familiar
  // 'p1 · [0...1] + p2 · [1...0]'
    : pts[0] * fn*idx
      + pts[1] * (1-fn*idx);

function b_curv(pts, n) =
// determine fn
  let (fn=
  // is n given? if so fn = n
  n ? n :
  // if no n is given,
  // are there two controlpoints?
  len(pts) == 2 ?
  // if yes: fn = 2
  2 :
  // and if no, calculate:
  length(pts)/fs)
  // now knowing fn,
  // call b_pts() and concatenate points
    [for (i= [0:fn])
      concat(b_pts(pts, 1/(fn-1), i))]; 

// points
p1 = [5.5, 0];
p2 = [1.5, 0];
p3 = [0, 2];
p4 = [0, 7];

// calculating the points
points = b_curv([p1, p2, p3, p4]);

// displaying the calculated points
rainbow(points);

// displaying points as a rainbow
module rainbow (points) {
  for (i= [0 : len(points)-1 ])
  color([cos(20*i)/2+0.5,  // red
        -sin(20*i)/2+0.5,  // green
        -cos(20*i)/2+0.5,  // blue
        1])                // alpha
translate(points[i]) sphere(0.5, $fn=10);
}

// displaying [p1 .. p4]
for (i=[p1, p2, p3, p4])
  translate(i) color("black")
    cylinder(1, 0.2, 0.2, $fn=10);
 

functions b_pts() and b_curv()

b_pts() contains the recursive mechanism and returns a number. It is called for each point separately. It is called with an array of points 'pts', a number in how many points the curve will be calculated 'fn', and a number which of the points will be calculated 'idx'.
It asks: 'Am I given more than two points in the array 'pts'?' And if so, it calls itself for the first to the second-last point multiplied by n·idx and adds calling itself for the second to the last point, multiplied with 1 - n·idx.
If the number of points in the array is two, it does the familiar 'p1 · [0...1] + p2 · [1...0]'

In b_curv(), which is called with an array of points 'pts' and an optional number n, the amount of points to calculate is determined, b_pts() called, and put everything into an array.

Uneven distance

As you can tell from the rendered file, the distance of the points is not perfectly even. But usually good enough since the points are closer by in places where the curve is tighter.

A hull() for the real life

The rainbow is lovely to display the points but in most cases we want something like this instead:

 for (i= [0 : len(points)-1])
    hull(){
       translate(points[i]) shape();
       translate(points[i+1]) shape();
    }
 

The most commonly used amount of points is four, this is also called 'cubic curve'. The first and the last point are the both ends of the curve and the points between make the curve curvy.

When a Bézier curve starts at one side, it first starts going towards the second point and then the influence of the third point grows stronger and so on. If differential calculus feels familiar to you, think of it as that the derivative function at the start of the curve points towards the second point.

And this is why, in typography, the start and end points of the curves are commonly set at

• the pointy ends of the letter and
• the most right, left, top and bottom points of a curvy shape.

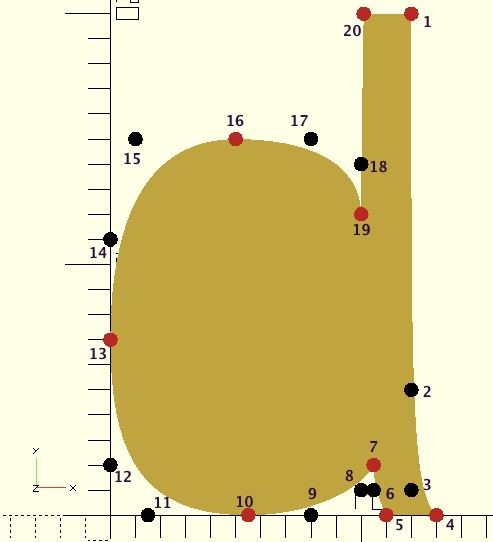
This can be observed in the image of the letter d, where the red dots are the starts and ends of the curves and the black dots are the points in-between.

Take a look at the bottom left curve of the letter d, between points 10 and 13. Notice that all four point are either on the x or the y axis. And now take a look at the two adjacent curves, 7-10 and 13-16. You'll notice that point 9 is located on the x axis as well and point 14 n the y-axis. Having point 9, 10 and 11 in one axis provides a smooth curve around point 10, and the easiest way to make that happen is locating all of them with the same y-value (0). Similarly, the continuous nature of the curve around point 13 ensures by points 12, 13 and 14 all having the same x-value (0).

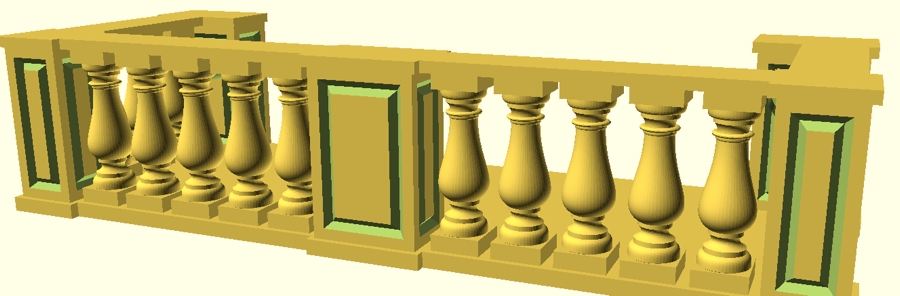
Bézier curves can be used for many things, for instance I made a balustrade balcony in OpenSCAD using Bézier curves, and it holds chalk for a blackboard now.

After the first, conceptual video, I made a second video with live-coding of a cactus-shaped cookie cutter.