A good approximation for the length of Bézier curves had been lacking for my OpenSCAD Bézier curve code and in December 2024 I fixed it. All the Jupyter notebook code is on GitHub.
I've approached it this way:
- Create Bézier curves from random points. Those curves look wild.
- Run linear regression with the distances of the points as x and the length as y. This made the formulae below.
- Test model on curves of my former design projects (cookie cutters). Works fine / good prediction.
Given a curve with the points labeled as such:
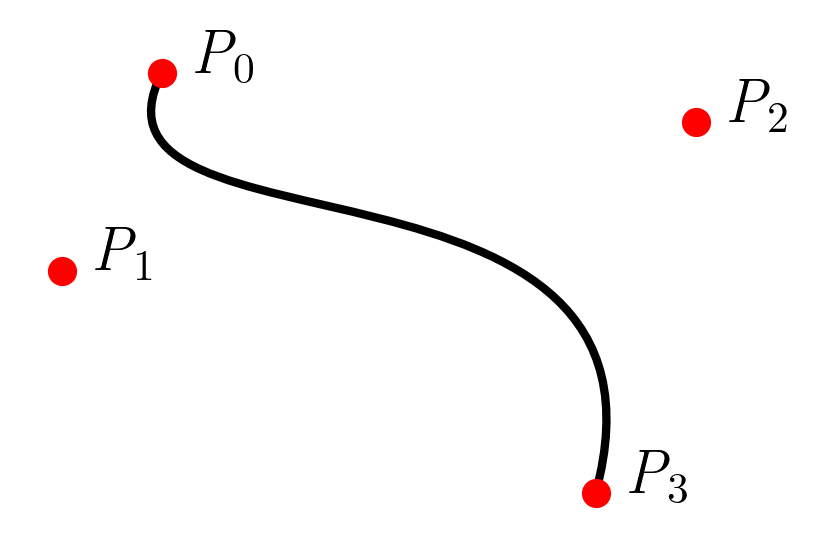
The formula for a curve with three points is:
L = 0.43 · |P0 - P1| + 0.53 · |P0 - P2| + 0.43 · |P1 - P2|
The formula for a curve with four points is:
L = 0.35 · |P0 - P1| + 0.40 · |P0 - P2| + 0.23 · |P0 - P3| - 0.09 · |P1 - P2| + 0.40 · |P1 - P3| + 0.35 · |P2 - P3|
The formula for a curve with five points is:
L = 0.32 · |P0 - P1| + 0.35 · |P0 - P2| + 0.23 · |P0 - P3| + 0.10 · |P0 - P4| - 0.13 · |P1 - P2| + 0.20 · |P1 - P3| + 0.23 · |P1 - P4| - 0.13 · |P2 - P3| + 0.35 · |P2 - P4| + 0.32 · |P3 - P4|
Three dimensions
The formulae that emerge from fitting with three dimensional Bézier curves are similar enough to the 2d ones that I would use the 2d formulae (those above). There is no test with 'real' data on the 3d curves though.
Trying to get it symmetrical
That the models are always asymmetrical bugged me a bit, and I tried
to solve it with once with Decimal instead of float and the other
times with forcing symmetry. None of them made me happy either and I
concluded that I'll
a) accept the formulae for now and
b) see this as a reason to learn more about machine learning in the
future.
A friend suggested trying float64 besides Decimal too.
Quadratic equations
Because why not I tried fitting with Quadratic equations too. This lead to overfitting though, so the formulae remain as they are above.
Text last updated: January 5th, 2025