Motivation: well functioning curves in OpenSCAD
In the sometimes slow OpenSCAD one has to be mindful of computing power and I had been unhappy with the approximation of the length of the curve in my Bézier curve code since it existed. Ideally I would like to have an f(x) shaped way to calculate the approximation but the recursive nature of Bézier curves is persistent.
ChatGPT makes coding so easy now that I could approach it with data-scienc-y methods, making it the first project where I analyze data in a Jupyter notebook as my own project. I made 1000 cubic Bézier curves based on random numbers and looked at the sums of lengths of the approximations of three, four and five points compared to the actual lengths. They gave me, on average, 1.14, 1.05 and 1.03 times too short lengths, with the dispersion being worse for less points too.
Then I looked at the edge cases (very long and very short approximations) and decided that they aren’t worth the hassle because they look weird and are unlikely to actually appear in a design project. Therefore I am happy with estimating the length of the Bézier curves by calculating an approximation of four points and summing up the distances between them.
The file with the calculations is here. If you judge my skill keep in mind that most of the code is written by ChatGPT.
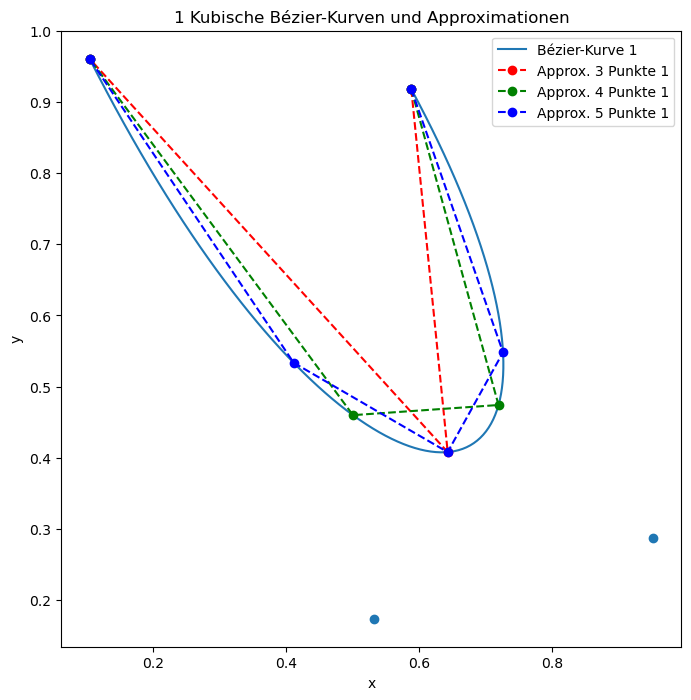
Later addition: linear formulae
Half a year later I ended up solving the problem in a more satifying way: I found Linear equations.
Text last updated: December 31st, 2024